Le Mystère des Cercles Noirs
The Cave Rings Mystery
Des spéléothèmes très particuliers par C. Ghommidh (2011-2012)
Les cercles parfaits tracés sur le sol de quelques cavités sont des spéléothèmes bien mystérieux. Rares de manière générale, ils peuvent être localement abondants. Nous avons eu l'occasion de rencontrer de telles formes à plusieurs reprises lors de nos expéditions au Laos. La première fois, en 2004, dans Tham Mo (appelée aussi Tham Pha Leusi, à Ban Vang Hin, vallée de la haute Nam Pakan), puis en 2007, dans Tham En (Ban Nong Ping, vallée de la Xé Bang Faï), enfin en 2008 dans la grotte des Nuages (réseau fossile de la Xé Bang Faï amont).


Photo 1 et 1bis - “Cercle noir” (cave ring) dans Tham En ( R. Huttler, 2008)
Ces spéléothèmes très particuliers ne sont cependant pas nouveaux. Brouquisse rapporte des observations similaires dans Tham Boumlou (Nam Pakan aval, Galerie des Sentinelles de pierre) en 2002. Au Nord-Laos, Renouard et col. (2001) signalent la présence de centaines de ces cercles dans Tham Lom, près de Van Vieng.
Ils ne sont pas non plus exclusifs au Laos, puisque quelques observations, réalisées au Brésil et en Italie ont été déjà publiées (Montanaro, 1992 ; Auler, 1993 ; Hill et Forti, 1998…). Le phénomène nous a paru suffisamment intéressant et inhabituel pour que, depuis 2008, nous procédions à une étude un peu approfondie de ses différents aspects.
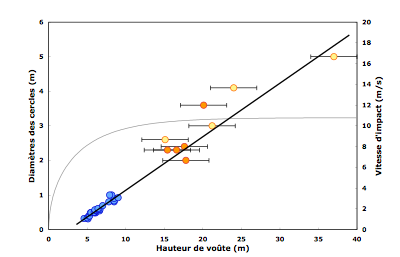
Figure 1 - Relation entre diamètre des cercles et hauteur de voûte dans Tham En. La couleur des points correspond à trois séries de mesures, dans des secteurs différents de la cavité. La vitesse d'impact (trait fin), calculée pour une goutte de 5 mm de diamètre, est également reportée sur le graphe.

Deux mécanismes ont été proposés pour expliquer ces formations. Hill et Forti (1998) pensent qu'il s'agit de projections liées à l'impact sur le sol des gouttes tombant de la voûte (splash rings). Cependant, il semble très peu probable que le mécanisme de formation puisse être celui d'un rebond. Il faudrait en effet que les gouttes rebondissent et soient fractionnées indépendamment de la nature et de la géométrie du sol, pour se déposer en cercles parfaits mesurant parfois plusieurs mètres de diamètre. La photo 2 montre que ce n’est pas ce qui habituellement constaté ! On pourrait admettre qu'exceptionnellement ce puisse être le cas, mais le fait que les cercles soient souvent observés en abondance sur des zones délimitées oblige à reposer le problème. Il s'agit d'un phénomène spécifique à certaines zones dans quelques cavités. Par ailleurs, le diamètre des cercles devrait être directement lié à la vitesse des gouttes lors de l'impact au sol. Cette vitesse augmente d'abord en fonction de la hauteur de chute suivant une relation v2 = 2 g.h, mais tend ensuite vers une valeur constante en raison du frottement avec l'air (force de traînée).
Photo 2 - Trajectoires aléatoires et asymétriques des gouttelettes projetées après l’impact d’une goutte au sol
Enfin, plusieurs observations montrent que les cercles se forment même lorsque l'impact au sol a lieu dans une anfractuosité empêchant les projections latérales. C'est ce que révèle de manière évidente le cercle brisé, déposé sur un bloc cassé, rencontré dans la Grotte des Nuages (branche fossile de la Xé Bang Faï souterraine) : vu de dessus, il présente l'aspect d'un cercle "classique", quoique discontinu, alors que la stalagmite se trouve une vingtaine de centimètres plus bas, entre les blocs. Vu de coté, on constate que le cercle s’est développé sur plusieurs niveaux, et en particulier sur le bloc le plus élevé.


Photo 3 et 3 bis - Le cercle brisé de la Grotte des Nuages, vu de dessus et de profil.
Le point d’impact est dans la fissure entre les blocs. Le compas est posé sur le bloc supérieur.
Cette expérience originale permet d'invalider totalement l'hypothèse de projections issues de l'impact au sol. Elle montre également que les cercles sont des spéléothèmes capables d'évolution rapide. Nozzoli et col. signalent cependant que les gouttes secondaires n'ont jamais été observées lors de leur expérience et que cette hypothèse n'explique pas pourquoi certaines stalactites forment des cercles et pas d'autres.
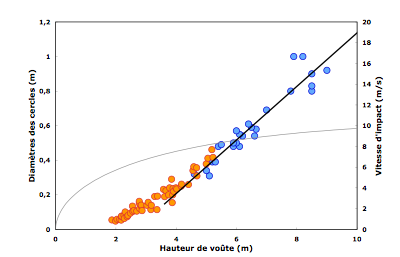
Un point remarquable est l'excellence de la concordance entre les mesures réalisées par Nozzoli et col. et celles que nous avons nous-même réalisées dans Tham En (Fig. 2). Alors que les deux jeux de données couvrent des gammes différentes de taille, la relation entre diamètre et hauteur de voûte est remarquablement continue. On constate que la relation quadratique que pensaient avoir mis en évidence Nozzoli et col. se prolonge en une droite. Par ailleurs, la modélisation mathématique de l’hypothèse de Montanaro ne permet pas de retrouver, même qualitativement, les résultats expérimentaux.
Figure 2 - Relation entre diamètre des cercles et hauteur de voûte dans Tham En. La vitesse d'impact, calculée pour une goutte de 5 mm de diamètre, est également reportée sur le graphe

Pour Richard Perkins, spécialiste de la turbulence et du transport des particules (Hunt et col. 2005), le fractionnement des gouttes, comme origine de la formation des cercles, est une hypothèse hautement improbable : pour obtenir des cercles aussi nets et aussi réguliers, il faudrait à la fois que la direction d'éjection soit parfaitement aléatoire et que la vitesse d'éjection soit parfaitement constante, couple invraisemblable de conditions (Perkins, 2010 - communication personnelle).
Photo 4 - Ambiance "brouillard" dans la galerie du Métro de Tham En
( R. Huttler, 2008)
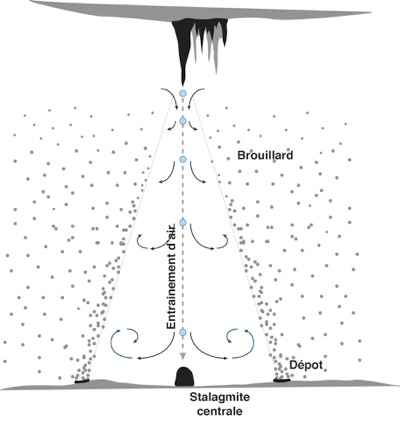
Le mécanisme pourrait ainsi être le suivant : dans leur chute, le train de gouttes perturbe l'atmosphère, provoquant un flux d’air descendant qui s'épanouit en écartant les microgouttelettes de brouillard (ou tout simplement les aérosols en suspension), de l'axe de la chute et en provoquant éventuellement leur accrétion. Le dépôt du brouillard serait alors concentré sur un anneau (fig. 3). La fréquence de chute des gouttes pourrait éventuellement être un facteur additionnel expliquant pourquoi les cercles n’apparaissent que sous certaines stalactites.
Figure 3 - Mécanisme proposé pour la formation des cercles noirs.
Une autre voie de validation, indirecte celle-là, consiste à rechercher un lien éventuel entre mécanisme de formation et composition du dépôt observé sur certains cercles. Nous avons procédé à un échantillonnage minimal du cercle qui illustre le début de cet article. Les prélèvements effectués en 2008 sur l’anneau ont été complétés en 2010 par un échantillonnage de la stalagmite centrale et des espaces intra- et extra- annulaires. La spectroscopie de rayonnement X en microscopie électronique à balayage a ensuite été utilisée pour obtenir la composition des échantillons. Alors que dans l'environnement immédiat, le concrétionnement comporte la présence de soufre (sulfates) en quantité suffisante pour que des aiguilles de gypse se forment, l'anneau n'en garde aucune trace. En revanche, il contient des quantités importantes de phosphore (phosphates), qu’on ne retrouve pas dans les autres échantillons.
Cette concentration anormalement élevée de phosphate est à rapprocher de la présence d'amas importants (plusieurs centaines de m2, sur une épaisseur supérieure au mètre) de guano d'hirondelles dans la galerie d'entrée. Ce guano est sec, pulvérulent et riche en phosphore. Des poussières entraînées loin dans la cavité pourraient servir de points de nucléation aux gouttelettes de brouillard. Leur dépôt par entraînement expliquerait la présence de phosphate au niveau de l'anneau. En l'absence de poussières, le dépôt de gouttelettes de brouillard entraîne simplement un nettoyage local du substrat. Le cercle apparaît alors sous la forme d'un anneau clair sur fond plus sombre.
Rares ? Pas tant que ça !
C’est au fond de la Cave de Vitalis, cavité bien connue sur la bordure du Causse du Larzac, autant dire dans notre jardin, que nous avons eu le plaisir de retrouver nos mystérieux cercles. Le premier, sur une coulée stalagmitique fortement inclinée, à proximité du Gour de la Tortue (ou de l’Oeuf au Plat), était très déformé. En revanche, le second, au fond de la Galerie du Lac, était parfait, même si moins spectaculaire que ses homologues laotiens. Du coup, nous avons mis à profit une visite dans les galeries “secrètes” de la grotte de Clamouse pour partir à la chasse aux cercles. Et nous n’avons pas été déçus, avec une dizaine de prises qui viennent gentiment compléter notre collection de mesures et s’y intégrer sans surprise. Dans chaque cas, les cercles se sont formés dans des secteurs des cavités peu ventilés, où un brouillard se forme temporairement.
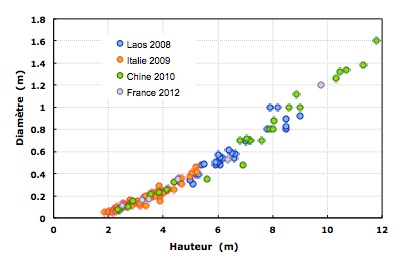
Figure 4 - Corrélation entre diamètre et hauteur de voute
C’est simple, leur diamètre (en mètres) est toujours à peu près égal à 0.14 x (hauteur - 2)... Bonne chasse ! Tenez nous au courant !
Bibliographie
Auler A., 1993. Les cercles de calcite de la "Lappa do Bezerra" (Sao Domingos, Goyas, Brésil). Karstologia, 22, 2, 55-56.
Brouquisse F., Faverjon M., 2005. Rapport d'exploration 2002-2004. CREI. Fédération Française de Spéléologie.
Eggers J., 2005. Drop formation – an overview. ZAMM. Z. Angew. Math. Mech. 85, 6, 400-410.
Gunn R., Gilbert D., 1949. The terminal velocity of fall for water droplets in stagnant air. J. Meteorology, 6, 243-248
Hill C., Forti, P., 1998. Cave minerals of the world (2nd ed.), Huntsville, Alabama, NSS.
Hunt J.C.R, Delfos R., Eames I., Perkins R.J., 2007. Vortices, Complex Flows and Inertial Particles. Flow Turbulence Combust., 79, 207–234.
Montanaro L., 1992. Osservazioni sui ‘‘cerchi’’ della Grotta del Sorell. Boll. Gr. Speleol. Sassarese, 13, 21–22.
Nozzoli F., Bevilacqua S., Cavallari L., 2009. The genesis of cave rings explained using empirical and experimental data. J. Cave and Karst Studies, 71, 2, 130–135.
Renouard L., Gillet M., Lapie G., Scherk G., 2001. Spélaologie 2000 – Rapport d'expédition CREI. Fédération Française de Spéléologie.
Sakiadis B.C., 1984. Fluid and particle mechanics. in Perry's Chemical Engineer Handbook, Perry, Green, Maloney Edts, McGraw-Hill, Paris, p. 5-27.
Villermaux E., Bossa B., 2009. Single-drop fragmentation determines size distribution of raindrops. Nature Physics, 5, 697-702.

